PROBLÉM:

1. Určení vlnových délek nejintezivnějších (nejjasnějších) spektrálních čar He.
2. Určení vlnových délek nejintenzivnějších spektrálních čar Hg

Experimentální uspořádání je na obrázku 1. Izolované držáky přívodu z výstupu napěťového zdroje 7 kV. Metrová škála je zabezpečena ve výšce štěrbiny ochrannou trubicí bezprostředně za spektrální trubicí.

TEORIE A VYHODNOCENÍ:

1. Když světlo vlnnové délky l dopadá na mřížku, která má mmmřížkovou konsatntu dochází k difrakci. Maxima intenzity se vyskytují v místech, kdy difrakční úhel vyhovuje podmínce.

Z obr. 2 máme

A proto

2) Dopadem elektronů se vyvolává excitace He a Hg atomů. Rozdíl energií tvořený návratem energií z exitovaného stavu E₁ do základního stavu E₀, se vytváří v podobě fotonu s frekvencí f

kde h = Planckova konstanta = 6,63 × 10^-34 J × s

Hamiltonovský operátor (nerelativistický) pro dva elektrony 1 a 2 atomu He je tvaru

kde

m a e odpovídají hmotnosti a náboji elektronu, místo

je Laplaceův operátor a je umístnění i-tého elektronu

Spin-orbitální energii můžeme v případě Z = 2 u helia zanedbat, protože je malá, pokud Z je malé. Uvažujeme – li

jako interaknčí člen elektron – elektron, potom vlastní hodnoty Hamiltonova operátoru bez interakce jsou stejné jako pro atom vodíku, pro n, m = 1, 2, … Jelikož pravděpodobnost přechodu pro současnou exitaci dvou elektronů je mnohem menší než pro exitaci jednoho elektronu, enrgetické spektrum systému bez interakce je

Interakční člen snímá degeneraci momentu hybnosti čistého vodíkového spektra a degeneraci výměné energie

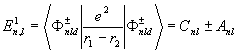Kde :

Jsou antisymetrizované neinterakční dvoučásticové vlnové funkce se symetrickou anebo antisymetrickou složkou koordináty

e^* je kvantové číslo momentu hybnosti a místa

• je nábor (množina) dalších kvantových čísel

V ukázaném případě orbitální moment jednoho elektronu l je roven celkovému momentu hybnostidvou elektronů L, protože jsou uvažovány pouze jednočásticové interakce a druhý elektron zůstává v základním stavu (l=0).

C_nl a A_nl jsou Coulombické resp. Výměnná energie, které jsou kladné. Vazba orbitálního momentu hybnosti L a celkovým spinem S dává pro S=0, tj. symetrickou složkou koordináty singletovou řadu, a pro S=1, tj antisymetrickou složkou koordináty pak bipletovou. Kvůli neexistenci spinu orbitální interakce je v tripleti rozštěpení jen málo. Nakolik narušené vlnové funkce jsou vlastní funkce pro S² a nakolik S² se mění s dipólovým operátorem, dává ho výběrové pravidlo D S = 0 (které je charakteristické pro 2 – elektronové systémy s nízkým jaderným nábojovým číslem) a zakazuje tak přechody mezi trypletovými a singletovými úrovněmi.

Navíc nezávisle od spin-orbitální interakce výběrové pravidlo pro celkový moment hybnosti D J=0, ± 1 platí s vyjímkou pro J=0 ® J^/=0. Pokud je spin-orbitální interakce malá, potom lze použít D L=0, ± 1. Detailní výpočet dává spektrum He na obr. 3.

Obr.3 Spektrum He

Tabulka 1 – Změřené spektrální čáry He a odpovídající přechody mezi energetickými hladinami.

Veličiny výměnné interakce a Coulombovské interakce dvou elektronů se mohou odhadnout porovnáním energií přechodů

Podobně He je i Hg dvouelektronový systém a je tvořený strukturou dvou sérií. Spin-orbitální interakce je ovšem relativně výrazná tak, že pouze celkový moment hybnosti J = L + S je "dobrým” parametrem zachování. Zvýrazněné je i štěpení uvnitř tripletu. Navíc se tu nedá použít výběrové pravidlo D S=0, protože S není "dobrý" parametr zachovávaný (přechod od L-S vazby k vazbě jj).

Obr. 4 Spektrum rtuti (Hg)

Tab. 2 Změřené spektrální čáry Hg a odpovídající přechody mezi energetickými hladinami.

Literatura:

PHYWE