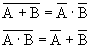3/6

Booleova algebra

Zákony pro logické operace:

  • komutativní:
 A+B = B+A
A.B = B.A 		 
  • asociativní:
 A+B+C = A+(B+C)=(A+B)+C
A.B.C=A.(B.C)=(A.B).C 		 
  • distributivní:
 A.(B+C)=A.B+A.C
A+(B.C)=(A+B).(A+C) 		 
  • dvojitá negace:
  
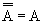
  • vyloučení třetího:
  
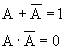
  • o agresivnosti:
 A+1 = 1
A.0 = 0 		 
  • o neutrálnosti:
 A+0=A
A.1=A 		 
  • absorpce:
 A+A = A
A.A = A
A+A.B =A
A.(A+B)=A
 A(1+B)=A.1=A
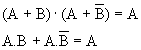
A.A+A.B=A+A.B=A(1+B)=A.1=A
  • absorpce negace:
  
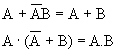
  • de Morganovy zákony: