Geometrické iluze

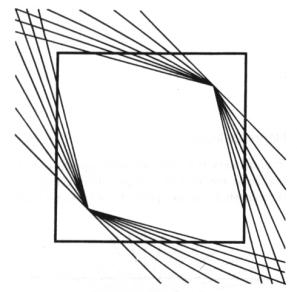
Heringův klam - Přetnutí silných úseček svazků paprsků vede k tomu, že se úsečky jeví jako prohnuté, ačkoliv jsou ve skutečnosti přímkami. K podobnému zkreslení může dojít i tehdy, když úsečky vytvoří např. čtverec. Když se čtverec přetne svazkem paprsků, vjemově se rozšiřuje. Většinu těchto klamů vysvětlujeme fyzikálně, například jako důsledek zvláštní konfigurace předmětů ve vjemovém poli. Toto vysvětlení je však příliš zjednodušeno.

Fraseova "spirala" -  Optický klam při kterém se kruhy jeví jako spirála. Pokusíte-li se sledovat prstem "spirálu" z různých bodů, vždy zjistíte, že jsou to kružnice. Klam je tak silný, že i po přezkoušení budete vidět spirálu a nikoli kruhy. Potíže můžete mít i při vlastním sledování kružnice pro silný vliv spirálového efektu, který je způsoben  mřížovou strukturou pozadí a šrafováním vlastních kruhů.

Hermanova mříž - Nazývá se taky kontrastním klamem. Průsečíky bílých mříží mezi černými čtvercovými plochami se jeví jako tmavší. Jestliže předlohu změníme tak, že mříž bude černá a čtverce bílé, pak průsečíky černé mříže se budou jevit jako světlejší.

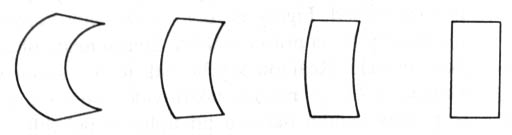
Vjem rotujícího obrazce - Při bezprostředním vnímání se účastní zraková paměť. Když přecházíme postupně od prvního ke čtvrtému obrázku, tak poslední tvar se nám na několik sekund nejeví jako plošný obdélník, ale hloubkově jakož to třidimenzionální tvar.

  Bolehlav - Tento název je poměrně výstižný, však zkuste sami. U tohoto obrázku se nám může zdát, že kruh vystupuje do popředí, nebo naopak, tvoří pozadí. Někdy se nám také zdá, že černá barva, která vyplňuje kruh je znatelně sytější. Záleží rovněž na tom, jak obrázek pozorujeme, jestli se soustředíme, nebo jestli se při pozorování pohybujeme.

Trošku zajímavá šachovnice. Ale jako rovnoběžky, tak i tohle je opět jenom klam. Šachovnice je doopravdy taková jako normálně...

"Neuvěřitelný" - Zdají se Vám být tyto čáry rovnoběžné? Ne? Opak je pravdou! Co způsobuje, že se nám zdá, že jsou čáry zakřivené? Je to kontrast dvou barev a vzájemné posunutí jejich čtverců.