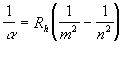Spektrum atomu vodíku

    Na základě rozptylu částic a formuloval Rutheford planetární model atomu , v němž je téměř celá hmota atomu soustředěna v malé kladně nabité centrální oblasti , tzv. jádru. Elektrony potom vytvářejí záporně nabitý obal. Aby elektrony nebyly v důsledku coulombovských sil k jádru přitaženy, musí obíhat kolem jádra takovou rychlostí, aby odstředivá síla byla v rovnováze s coulombovskou silou.

    Tento model se však dostává do sporu s klasickou elektrodynamikou.soustava elektron - jádro tvoří elektrický dipól s proměnným dipólovým momentem, takže podle klasické teorie elektromagnetického pole vyzařuje energii, která musí jít na účet celkové energie atomu, což by vedlo ke zmenšování poloměru dráhy elektronu až nakonec k jeho splynutí s jádrem. Podle výpočtů by doba života takového atomu byla » 10^-16, což je v rozporu se skutečností. Navíc by vysílané záření mělo mít spojitý charakter, což bylo rovněž v rozporu se známými fakty.

    Pro posuzování správnosti základních modelových představ se nejlépe hodí atom vodíku vzhledem ke své jednoduchosti. Při pozorování světla emitovaného doutnavým výbojem ve vodíku byly ve viditelné oblasti pozorovány čtyři spektrální čáry a v ultrafialové oblasti dalších dvacet, které s těmito čtyřmi přímo souvisí. Balmer roku 1889 odvodil empirický vztah pro vlnové délky jednotlivých čar této série.

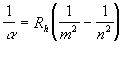          (1)

kde R_h je empirická konstanta (tzv. Rydbergova konstanta), jejíž hodnota je R_h=1,09737.107m -1. Později byly v infračervené a ultrafialové oblasti objeveny ještě další série; jejich vlnové délky značí číslo série: m=1 - Laymanova, m=2 - Balmerova, m=3 - Paschenova, m=4 - Bracketova a m=5 - Pfundova.

    Potíže Ruthefordova planetárního modelu odstranil roku 1913 Niels. Bohr na základě zákonitostí spektra atomu vodíku a kvantové teorie světla formuloval základní postuláty a z nich odvozoval na základě klasické fyziky další důsledky:

1. Atomy se nacházejí v ustálených energetických stavech, ve kterých neabsorbují ani neemitují energii.
2. 2p násobek momentu hybnosti obíhajícího elektronu se rovná celistvému násobku Planckovy konstanty h.
3. Atom emituje nebo absorbuje záření po kvantech při přechodu z jednoho stacionárního stavu do druhého. Toto záření je monochromatické a jeho frekvence je dána rozdílem energie počátečního a konečného stavu atomu

          (2)

    Velkým úspěchem Bohrovy teorie bylo, že dokázala kvantitativně vysvětlit zákonitosti spektra atomu vodíku.

    Na základě Bohrových představ se dá odvodit vztah pro spektrum atomu vodíku.

    Pro elektron na i-té stacionární dráze platí

2p r_imv_i = ih          (3)

kde i je přirozené číslo, m hmotnost elektronu, v_i jeho rychlost na i-té dráze a h Planckova konstanta. Rovnováhu mezi odstředivou a Coulombovskou silou vyjadřuje podmínka

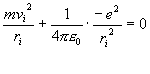          (4)

    Z rovnice (3) vyjádříme v_i, dosadíme do rovnice (4) a po jednoduché úpravě získáme podmínku pro poloměr i-té dráhy

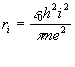          (5)

    Celková energie elektronu na i-té dráze je dána součtem jeho kinetické a potenciální energie. Výraz pro kinetickou energii získáme z rovnice (4) vynásobením členem a dosazením rovnice (5) za r_i. Po provedení naznačených úprav získáme

          (6)

    Elektron se nalézá v elektrickém poli jádra, které lze z hlediska elektrostatických účinků považovat za bodový náboj, takže s přihlédnutím k rovnici (5) potenciální energie elektronu v poli jádra je

          (8)

    Celková energie elektronu na i-té dráze je podle rovnic (7) a (8)

          (9)

    Celková energie elektronu vázaná v atomu je záporná; nejvyšší, tj. nulové hodnoty nabývá pro i® Ą , což odpovídá zřejmě základnímu stavu. Při přechodu z jednoho stavu do druhého vyzáří elektron podle 3. postulátu kvantum energie. Vyjádříme-li kmitočet vyzářeného kvanta podle rovnice (2), kam za E_n a E_m dosadíme podle vztahu(9) a zavedeme vlnovou délku podle vztahu ,dostaneme

          (10)

kde m a n jsou přirozená čísla určující příslušné energetické hladiny. Výraz před závorkou je tvořen pouze univerzálními konstantami.

    Bohrova teorie znamenala důležitý krok při zjišťování struktury atomu.

DALŠÍ